Constants

03D Computability and recursion theory

Busy Beaver ones function

OrdinaryArtery, via Wikimedia Commons. CC BY-SA 4.0.

The Busy Beaver ones function $\Sigma(n)$ (Rado’s sigma function) is the maximal number of 1s that an n-state Turing machine can print on an initially blank tape before eventually halting.

Wikipedia Wikidata MathWorld OEIS

Compilation status: Initial

$3.5\times10^{18267}$
$?$

$10^{10^{10^{10^{18705353}}}}$
$?$

Busy Beaver shift function

Simplified spacetime diagram of the fifth busy beaver machine

--MULLIGANACEOUS--, via Wikimedia Commons. Public domain.

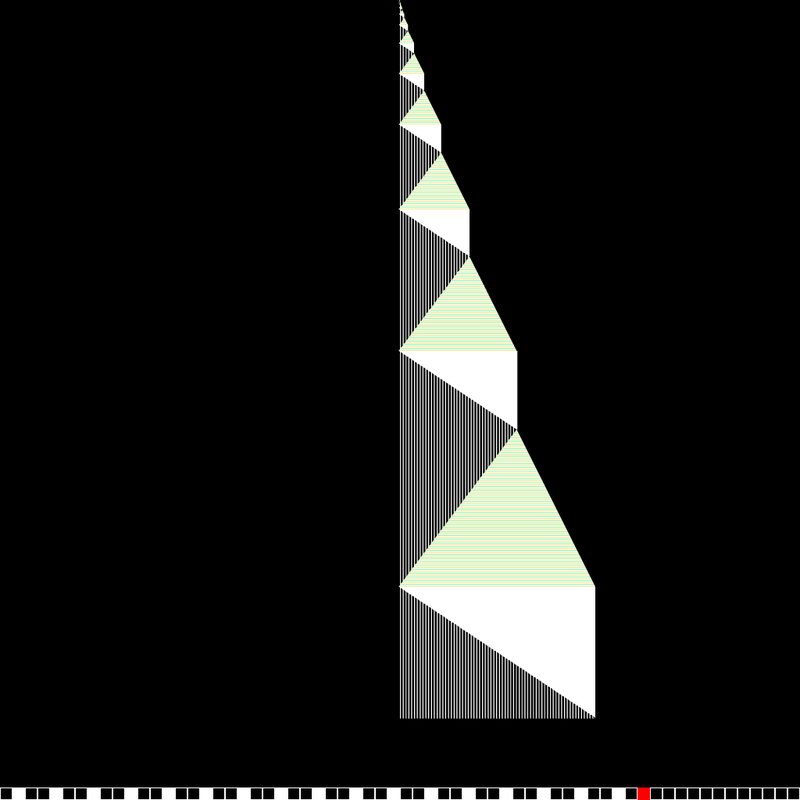
The Busy Beaver shift function $BB(n)$ ($S(n)$) is the maximal number of steps that an n-state Turing machine can make on an initially blank tape before eventually halting.

Wikipedia Wikidata MathWorld OEIS

Compilation status: Initial

$7.4\times10^{36524}$
$?$

$10^{2\times10^{10^{10^{18705353}}}}$
$?$

05A Enumerative combinatorics

Minimal superpermutation problem

The distribution of permutations in a 3 symbol superpermutation

IntegralPython, via Wikimedia Commons. CC BY-SA 4.0.

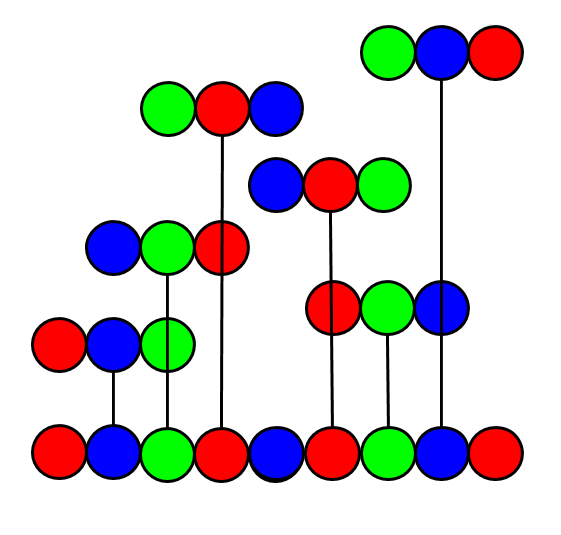
$L(n)$ is the shortest length of a string that contains each permutation of $n$ symbols as a substring.

Wikipedia Wikidata

Compilation status: Initial

Stamp folding

Robert Dickau, via Wikimedia Commons. CC BY-SA 3.0.

The number of distinct ways to fold a strip of $n$ labeled stamps.

Wikipedia Wikidata MathWorld OEIS

Compilation status: Initial

05C Graph theory

Cages

David Benbennick, via Wikimedia Commons. Public domain.

$n(k,g)$ is the order of a $(k,g)$-cage, a $k$-regular graph of girth $g$ of minimum order.

Wikipedia MathWorld

Compilation status: Initial

k\g	3	4	5	6	7	8	9	10	11	12	13	14	15	16
3	$4$	$6$	$10$	$14$	$24$	$30$	$58$	$70$	$112$	$126$	$202$ $272$	$258$ $384$	$384$ $620$	$512$ $960$
4	$5$	$8$	$19$	$26$	$67$	$80$	$?$ $275$	$?$ $384$	$?$ $?$	$728$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
5	$6$	$10$	$30$	$42$	$?$ $152$	$170$	$?$ $?$	$?$ $1296$	$?$ $2688$	$2730$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
6	$7$	$12$	$40$	$62$	$?$ $294$	$312$	$?$ $?$	$?$ $?$	$?$ $?$	$7812$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
7	$8$	$14$	$50$	$90$	$?$ $?$	$?$ $672$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $32928$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
8	$?$ $?$	$?$ $?$	$67$ $80$	$114$	$?$ $?$	$?$ $800$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $39216$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
9	$?$ $?$	$?$ $?$	$86$ $96$	$146$	$?$ $1152$	$?$ $1170$	$?$ $?$	$?$ $?$	$?$ $74752$	$?$ $74898$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
10	$?$ $?$	$?$ $?$	$103$ $124$	$182$	$?$ $?$	$?$ $1640$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $132860$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
11	$?$ $?$	$?$ $?$	$124$ $154$	$224$ $240$	$?$ $?$	$?$ $2618$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $319440$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
12	$?$ $?$	$?$ $?$	$147$ $203$	$266$	$?$ $?$	$?$ $2928$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $354312$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
13	$?$ $?$	$?$ $?$	$174$ $230$	$314$ $336$	$?$ $?$	$?$ $4342$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $738192$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
14	$?$ $?$	$?$ $?$	$199$ $288$	$366$	$?$ $?$	$?$ $4760$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $804468$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
15	$?$ $?$	$?$ $?$	$230$ $312$	$422$ $462$	$?$ $?$	$?$ $7648$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $1957376$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
16	$?$ $?$	$?$ $?$	$259$ $336$	$482$ $504$	$?$ $?$	$?$ $8092$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $2088960$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
17	$?$ $?$	$?$ $?$	$294$ $448$	$546$	$?$ $?$	$?$ $8738$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $2236962$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
18	$?$ $?$	$?$ $?$	$327$ $480$	$614$	$?$ $?$	$?$ $10440$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $3017196$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
19	$?$ $?$	$?$ $?$	$364$ $512$	$686$ $720$	$?$ $?$	$?$ $13642$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $4938480$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
20	$?$ $?$	$?$ $?$	$403$ $576$	$762$	$?$ $?$	$?$ $14480$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $5227320$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$

Degree-diameter problem

$N(d,k)$ is the largest possible number of vertices in a graph of maximum degree $d$ and diameter $k$.

Wikipedia Wikidata MathWorld

Compilation status: Initial

d\k	2	3	4	5	6	7	8	9	10
3	$10$	$20$	$38$	$70$ $?$	$132$ $?$	$196$ $?$	$360$ $?$	$600$ $?$	$1250$ $?$
4	$15$	$41$ $?$	$98$ $?$	$364$ $?$	$740$ $?$	$1320$ $?$	$3243$ $?$	$7575$ $?$	$17703$ $?$
5	$24$	$72$ $?$	$212$ $?$	$624$ $?$	$2772$ $?$	$5516$ $?$	$17030$ $?$	$57840$ $?$	$187056$ $?$
6	$32$	$111$ $?$	$390$ $?$	$1404$ $?$	$7917$ $?$	$19383$ $?$	$76891$ $?$	$331387$ $?$	$1253615$ $?$
7	$50$	$168$ $?$	$672$ $?$	$2756$ $?$	$12264$ $?$	$53020$ $?$	$249660$ $?$	$1223050$ $?$	$6007230$ $?$
8	$57$ $?$	$253$ $?$	$1100$ $?$	$5115$ $?$	$39672$ $?$	$131137$ $?$	$734820$ $?$	$4243100$ $?$	$24897161$ $?$
9	$74$ $?$	$585$ $?$	$1640$ $?$	$8268$ $?$	$75893$ $?$	$279616$ $?$	$1697688$ $?$	$12123288$ $?$	$65866350$ $?$
10	$91$ $?$	$650$ $?$	$2331$ $?$	$13203$ $?$	$134690$ $?$	$583083$ $?$	$4293452$ $?$	$27997191$ $?$	$201038922$ $?$
11	$104$ $?$	$715$ $?$	$3200$ $?$	$19620$ $?$	$156864$ $?$	$1001268$ $?$	$7442328$ $?$	$72933102$ $?$	$600380000$ $?$
12	$133$ $?$	$786$ $?$	$4680$ $?$	$29621$ $?$	$359772$ $?$	$1999500$ $?$	$15924326$ $?$	$158158875$ $?$	$1506252500$ $?$
13	$162$ $?$	$856$ $?$	$6560$ $?$	$40488$ $?$	$531440$ $?$	$3322080$ $?$	$29927790$ $?$	$249155760$ $?$	$3077200700$ $?$
14	$183$ $?$	$916$ $?$	$8200$ $?$	$58095$ $?$	$816294$ $?$	$6200460$ $?$	$55913932$ $?$	$600123780$ $?$	$7041746081$ $?$
15	$187$ $?$	$1215$ $?$	$11712$ $?$	$77520$ $?$	$1417248$ $?$	$8599986$ $?$	$90001236$ $?$	$1171998164$ $?$	$10012349898$ $?$
16	$200$ $?$	$1600$ $?$	$14640$ $?$	$132496$ $?$	$1771560$ $?$	$14882658$ $?$	$140559416$ $?$	$2025125476$ $?$	$12951451931$ $?$
17	$274$ $?$	$1610$ $?$	$19040$ $?$	$133144$ $?$	$3217872$ $?$	$18495162$ $?$	$220990700$ $?$	$3372648954$ $?$	$15317070720$ $?$
18	$274$ $?$	$1620$ $?$	$23800$ $?$	$171828$ $?$	$4022340$ $?$	$26515120$ $?$	$323037476$ $?$	$5768971167$ $?$	$16659077632$ $?$
19	$338$ $?$	$1638$ $?$	$23970$ $?$	$221676$ $?$	$4024707$ $?$	$39123116$ $?$	$501001000$ $?$	$8855580344$ $?$	$18155097232$ $?$
20	$381$ $?$	$1958$ $?$	$34952$ $?$	$281820$ $?$	$8947848$ $?$	$55625185$ $?$	$762374779$ $?$	$12951451931$ $?$	$78186295824$ $?$

05D Extremal combinatorics

Ramsey numbers

Cmglee, via Wikimedia Commons. CC BY-SA 4.0.

Ramsey number $R(r,s)$ is the smallest number $n$ such that any two-coloring of the edges of the complete graph $K_n$ must contain either a monochromatic $K_r$ in the first color or a monochromatic $K_s$ in the second color.

Wikipedia Wikidata MathWorld Metamath MSC2020 PlanetMath

Compilation status: Sourced

r\s	3	4	5	6	7	8	9	10	11	12	13	14	15
3	$6$	$9$	$14$	$18$	$23$	$28$	$36$	$40$ $41$	$47$ $50$	$53$ $59$	$60$ $68$	$67$ $77$	$74$ $87$
4		$18$	$25$	$36$ $40$	$49$ $58$	$59$ $79$	$73$ $105$	$92$ $135$	$102$ $170$	$128$ $210$	$138$ $256$	$147$ $307$	$158$ $364$
5			$43$ $46$	$59$ $85$	$80$ $133$	$101$ $193$	$133$ $282$	$149$ $381$	$183$ $511$	$203$ $672$	$233$ $860$	$267$ $1081$	$275$ $1341$
6				$102$ $160$	$115$ $270$	$134$ $423$	$183$ $651$	$204$ $944$	$262$ $1346$	$294$ $1855$	$347$ $2499$	$?$ $3301$	$401$ $4305$
7					$205$ $492$	$219$ $832$	$252$ $1368$	$292$ $2119$	$405$ $3197$	$417$ $4665$	$511$ $6653$	$?$ $9260$	$?$ $12635$
8						$282$ $1518$	$329$ $2662$	$343$ $4402$	$457$ $7040$	$?$ $10836$	$817$ $27485$	$?$ $41525$	$873$ $63609$
9							$565$ $4956$	$581$ $8675$	$?$ $14631$	$?$ $38832$	$?$ $64864$	$?$ $?$	$?$ $?$
10								$798$ $16064$	$?$ $45881$	$?$ $81123$	$?$ $?$	$?$ $?$	$1313$ $?$

Van der Waerden numbers

$W(r,k)$ is the smallest number $n$ such that if the integers $1$ to $n$ are colored with $r$ colors, there must be a monochromatic arithmetic progression of length $k$.

Wikipedia Wikidata MathWorld

Compilation status: Initial

r\k	3	4	5	6	7	8	9	10	11
2	$9$	$35$	$178$	$1132$	$3704$ $?$	$11496$ $?$	$41266$ $?$	$103475$ $?$	$193942$ $?$
3	$27$	$293$	$2174$ $?$	$11192$ $?$	$48812$ $?$	$238401$ $?$	$932746$ $?$	$4173725$ $?$	$18603732$ $?$
4	$76$	$1049$ $?$	$17706$ $?$	$157210$ $?$	$2284752$ $?$	$12288156$ $?$	$139847086$ $?$	$1189640579$ $?$	$3464368084$ $?$
5	$171$ $?$	$2255$ $?$	$98742$ $?$	$786741$ $?$	$15993258$ $?$	$86017086$ $?$	$978929596$ $?$	$8327484047$ $?$	$38108048914$ $?$
6	$226$ $?$	$9779$ $?$	$98749$ $?$	$1555550$ $?$	$111952800$ $?$	$602119596$ $?$	$6852507166$ $?$	$58292388323$ $?$	$419188538044$ $?$

52C Discrete geometry

Arrangements of lines in the affine plane

Mik, via Wikimedia Commons. CC BY-SA 3.0.

The number of ways of arranging $n$ lines in the (affine) plane.

OEIS

Compilation status: Initial

Arrangements of lines in general position

All arrangements of five lines in general position

Jon Wild and Laurence Reeves, via OEIS. OEIS terms of use.

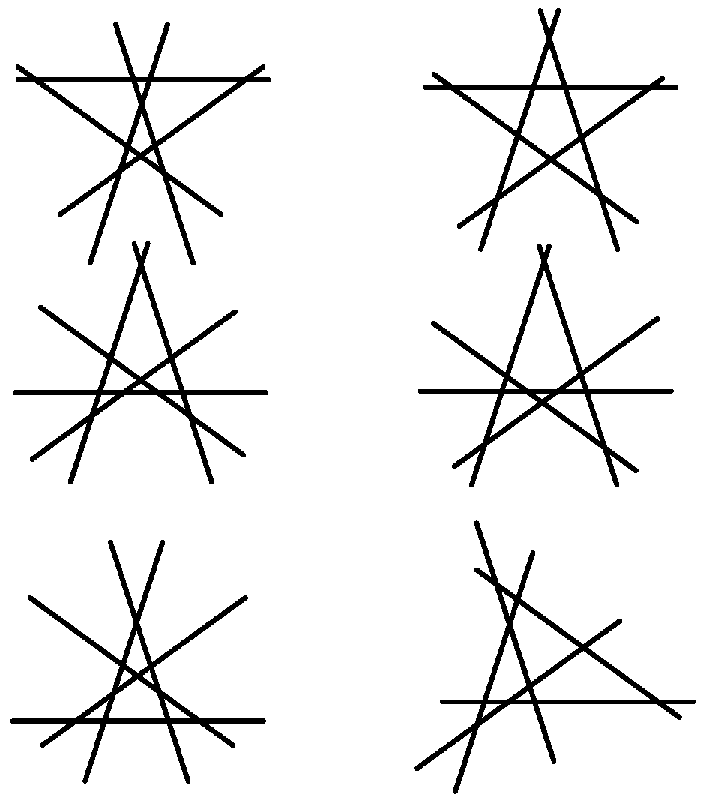
The number of ways of arranging $n$ straight lines in general position in the (affine) plane.

OEIS

Compilation status: Initial

Circle packing in an equilateral triangle

Packing 11 unit circles in an equilateral triangle

OwOUwUOwU, via Wikimedia Commons. CC BY-SA 4.0.

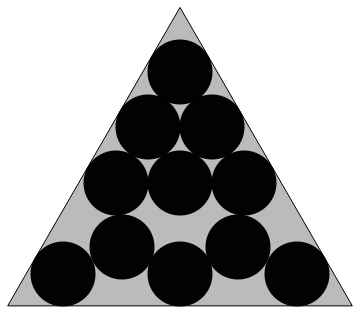
The side length of the smallest equilateral triangle into which $n$ unit circles can be packed.

Wikipedia

Compilation status: Initial

$2+2\sqrt{3}+\frac{2\sqrt{33}}{3}$

$6+2\sqrt{3}$

$4+2\sqrt{3}+\frac{4\sqrt{6}}{3}$

$4+4\sqrt{3}$

$?$
$4+\frac{2\sqrt{6}}{3} + \frac{10\sqrt{3}}{3}$

$?$
$8+2\sqrt{3}$

$8+2\sqrt{3}$

Disk covering problem

The smallest value $r(n)$ such that $n$ disks of radius $r(n)$ can be arranged to cover the unit disk.

Wikipedia MathWorld

Compilation status: Initial

Kissing numbers

Robertwb at English Wikipedia, via Wikimedia Commons. CC BY-SA 3.0.

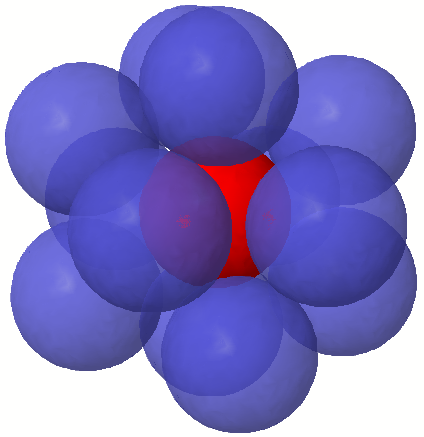
The kissing number of $\mathbb{R}^n$ is the maximum number of non-overlapping unit spheres that can touch a central unit sphere in $\mathbb{R}^n$.

Wikipedia Wikidata MathWorld

Compilation status: Initial

Map folding

Robert Dickau, via Wikimedia Commons. CC BY-SA 3.0.

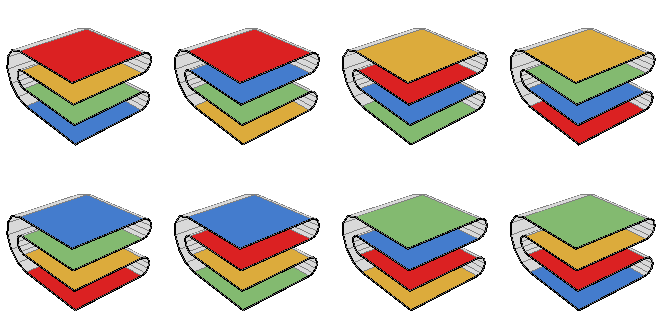
The number of distinct ways to fold an $m \times n$ rectangle into a unit square.

Wikipedia Wikidata MathWorld OEIS

Compilation status: Initial

m\n	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
2	$8$	$60$	$320$	$1980$	$10512$	$60788$	$320896$	$1787904$	$9381840$	$51081844$	$266680992$	$1429703548$	$7432424160$	$39409195740$	$204150606976$	$1073644675448$	$5545305620064$
3		$1368$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
4			$300608$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
5				$186086600$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
6					$123912532224$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$
7						$129950723279272$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$	$?$ $?$

Packing unit squares in a square

Optimal packing of 5 unit squares in a square

Amit6, via Wikimedia Commons. Public domain.

$s(n)$ is the side of the smallest square into which $n$ unit squares can be packed.

Wikipedia Wikidata MathWorld

Compilation status: Initial

$1$

$2$

$2 + \frac{1}{\sqrt{2}}$

$3$

$3 + \frac{1}{\sqrt{2}}$

$2 + \frac{4}{\sqrt{5}}$
${\approx}3.8771$

$2 + \frac{4}{\sqrt{5}}$
$4$

$3.8437$
$4$

$4$

$\frac{40\sqrt{2}+19}{17}$
${\approx}4.6756$

$\frac{40\sqrt{2}+19}{17}$
$\frac{7+\sqrt{7}}{2}$

$6\sqrt{2}-4$
$3+\frac{4\sqrt{2}}{3}$

$2\sqrt{2}+\frac{27+2\sqrt{10}}{13}$
$\frac{7}{2}+\frac{3\sqrt{2}}{2}$

$2\sqrt{2}+\frac{27+2\sqrt{10}}{13}$
$5+\frac{1}{\sqrt{2}}$

$2\sqrt{2}+\frac{6}{\sqrt{5}}$
$3+2\sqrt{2}$

$2\sqrt{2}+\frac{6}{\sqrt{5}}$
${\approx}5.9344$

$2\sqrt{2}+\frac{6}{\sqrt{5}}$
$6$

$5.6415$
$6$

$?$
$6$

$6$

$2\sqrt{2}+\frac{113+10\sqrt{3}}{37}$
${\approx}6.5987$

$2\sqrt{2}+\frac{113+10\sqrt{3}}{37}$
$6+\frac{1}{\sqrt{2}}$

$2\sqrt{2}+\frac{113+10\sqrt{3}}{37}$
${\approx}6.8189$

$2\sqrt{2}+\frac{8}{\sqrt{5}}$
$4+2\sqrt{2}$

$2\sqrt{2}+\frac{8}{\sqrt{5}}$
${\approx}6.9473$

$?$
$7$

$7$

$2\sqrt{2}+\frac{101+3\sqrt{14}}{25}$
${\approx}7.5987$

$2\sqrt{2}+\frac{101+3\sqrt{14}}{25}$
${\approx}7.7044$

$2\sqrt{2}+\frac{101+3\sqrt{14}}{25}$
$7+\frac{1}{\sqrt{2}}$

$2\sqrt{2}+\frac{101+3\sqrt{14}}{25}$
${\approx}7.8231$

$?$
${\approx}7.8488$

$?$
${\approx}7.9871$

$?$
$8$

$8$

$2\sqrt{2}+\frac{71}{13}$
$5+\frac{5}{\sqrt{2}}$

$2\sqrt{2}+\frac{71}{13}$
$3+4\sqrt{2}$

$2\sqrt{2}+\frac{71}{13}$
$8+\frac{1}{\sqrt{2}}$

$2\sqrt{2}+\frac{71}{13}$
$\frac{15}{2}+\frac{\sqrt{7}}{2}$

$?$
${\approx}8.8562$

$?$
${\approx}8.9121$

$?$
${\approx}8.9633$

$?$
$9$

$9$

${\approx}9.2667$
$6+\frac{5}{\sqrt{2}}$

${\approx}9.2667$
$4+4\sqrt{2}$

${\approx}9.2667$
$9+\frac{1}{\sqrt{2}}$

${\approx}9.2667$
$\frac{11}{2}+3\sqrt{2}$

$?$
$\frac{17+\sqrt{7}}{2}$

$?$
${\approx}9.8520$

$?$
${\approx}9.9018$

$?$
$5+\frac{7}{\sqrt{2}}$

$?$
$10$

$10$

100

$10$

11 Number theory

de Bruijn-Newman constant

The de Bruijn-Newman constant $\Lambda$ is defined via the zeros of a certain function $H(\lambda,z)$, where $\lambda$ is a real parameter and $z$ is a complex variable. More precisely, $H(\lambda, z):=\int_{0}^{\infty} e^{\lambda u^{2}} \Phi(u) \cos (z u) \, du$, where $\Phi$ is the super-exponentially decaying function $\Phi(u) = \sum_{n=1}^{\infty} (2\pi^2n^4e^{9u}-3\pi n^2 e^{5u} ) e^{-\pi n^2 e^{4u}}$ and $\Lambda$ is the unique real number with the property that $H$ has only real zeros if and only if $\lambda\geq \Lambda$.

Wikipedia Wikidata MathWorld

Compilation status: Sourced

$\ge 0$
$\le 0.2$